21 Birthday Problems
This was the first and most green Problem Set. It teetered on the edge of Higher Secondary and Recreational mathematics:
The winner was Aarav Bajaj, by a narrow margin of a single mark.
In second place was an ex-student of mine, Jisu Song.
The prizes were \$50 and $20 respectively.
Question 1
Prove that \(\frac{1}{0}\) is undefined.
Assume the negation of the statement: \(\frac{1}{0}\) is defined, s.t. \(\frac{1}{0} = x\). Algebraically swapping the \(x\) and \(0\), we can plot the graph for \(y=\frac{1}{x}\) at \(y=0\):
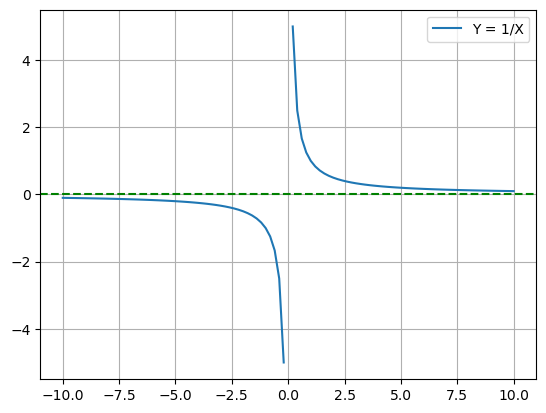
Now clearly the dotted line never touches the blue curve, and thus at no point does \(0 = \frac{1}{x} \implies \) that our initial assumption was false.
In conclusion, \(\frac{1}{0}\) is undefined.
Q2
RTP: \[\sin^2(\theta) + \cos^2(\theta) = 1\]
Proof:
By definition, \(\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\) and \(\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}\).
And \[\sin^2(\theta) + \cos^2(\theta) = \frac{\text{opposite}^2 + \text{adjacent}^2}{\text{hypotenuse}^2}\]
Furthermore, by the Pythagorean Theorem on the following figure, we have \(\text{opposite}^2 + \text{adjacent}^2 = \text{hypotenuse}^2\)
And thus \(\frac{\text{hypotenuse}^2}{\text{hypotenuse}^2} = 1\), which was that to be proved. \(\square\)
Q2.1
Dividing this equation through \(\sin^2(\theta)\):
\[\begin{align*} \frac{\sin^2(\theta)}{\sin^2(\theta)} +\frac{\cos^2(\theta)}{\sin^2(\theta)} &= \frac{1}{\sin^2(\theta)}\\ \implies 1 + \cot^2(\theta) &= \csc^2(\theta)\text{, as required} \end{align*}\]
Q3
\[\begin{align*} 1+\dots +1000 &= (1000+1) + (999+2) + \dots + (501 + 500)\\ &= \underbrace{1001 + 1001 + \dots + 1001}_{\text{50}\times}\\ &= 1001\times 500\\ &= 500500 \end{align*}\]
Q4
Tracing the most optimal path on the cube we have the red dotted line on the cube:
Which constructs 2 identical triangles which look like:
We can calculate their lengths with Pythagoras: \[\begin{align*}x &= \sqrt{(\frac{1}{4})^2 + 1^2}\\&=\frac{\sqrt{17}}{4}\end{align*}\] We then multiply this by 2 to get the total length: \(\frac{\sqrt{17}}{2} \approx 2.061\).
Q5
Hexagonal Packing.
We can split the rhombus into two equilateral triangles.
Then, by the Pythagorean Theorem, we find the height of one of these such triangles to be \(\sqrt{3}\).
Thus \[A_\Delta = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{\cancel{2}}\times \cancel{2} \times \sqrt{3} = \sqrt{3}\]
and \(A_\mathrm{rhombus} = 2\sqrt{3}\).
Now the area the rhombus takes up from each of the circles is for A, B, C, D: \(\left[\frac{1}{6} + \frac{2}{6} + \frac{2}{6} + \frac{1}{6} \right]\times \pi r^2 = 1\times \pi \times 1 = \pi\).
This is by nature of the hexagonal packing.
Finally, the ratio of the circle coverage to the total shaded area is \[\frac{\pi}{2\sqrt{3}} \approx 90.7%\]
Q6
Given that we redefine our notion of dimensionality for fractals to be \[\text{number of copies} = (\text{magnification factor})^d\]
Then clearly from
we see that each subsequent fractal contains 3 of the previous and thus the "number of copies" = 3. Then by considering the side lengths we see that upon each subsequent iteration it is doubling in length, implying that the "magnification factor" is 2. Now our equation becomes \[\begin{align*} 3 &= 2^d\\ \implies d &= \log_2{3}\\ &\approx 1.585 \end{align*}\]
An interesting result no?
Q7
Assume the negation; that \(\sqrt{2}\) is rational. Then \(\sqrt{2} = \frac{p}{q} \implies 2 = \frac{p^2}{q^2} \implies 2q^2 = p^2\).
This quantity on the left will always produce an even number, say \(2a\), and \(p^2\) will always be another number, say \(b\).
Thus we have \(2a = b \implies \frac{b}{a} = 2\).
Here we have violated our assumption because in simplifying \(\frac{b}{a}\) to 2, which means a common factor of 2 exists.
Thus \(\sqrt{2}\) is irrational. \(\square\)
Q8
Q9
Tangent line: \(y=9x-16\), Normal line: \(y=-\frac{1}{9}+\frac{20}{9}\).
Q10
\[p(x)=2x^3-11x^2+14x+10\] And given that \(p(3+i) = 0\), by the Conjugate Root Theorem we have \(p(3-i)=0\) and consequently
\[\begin{align*} (x-3-i)(x-3+i)\,c(x) &= 0\\ (x^2-6x+10)(ax+b) &= 2x^3 - 11x^2 +14x +10\\ &\implies a=2, b=1\qquad\text{(by comparing coefficients)}\\ \implies p(x) &= (x-(3-i))(x-(3+i))(2x+1)\\ \end{align*}\]
And so \(p(x)\) has roots \(3\pm i, -0.5\).
Q11
\[\large \int(e^{t^2} + 16)\,\, t\,\, e^{t^2} \mathrm{d}t = \frac{1}{2}\left( \frac{e^{t^2}+16}{2} \right )^2 + C\]
Q12
\[\large \int \tan(t)\sec^2(t) \mathrm{d}t = \frac{\tan^2(t)}{2} + C\] Note that this is equivalent to \(\frac{\sec^2(t)}{2} + C\) because the two functions only differ by a constant.
Q13
To sketch \(\frac{1}{(x-3)(x-4)}\) we can first sketch the quadratic on the denominator, and then reciprocate a few significant values to see what the shape of our desired sketch should be (\(x=-\infty,3,4,3.5,4.5,+\infty\)).
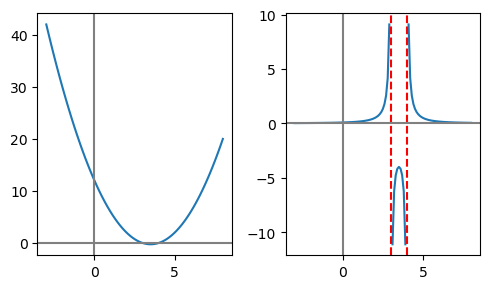
Q14
IMPORTANT: there are 2 mistakes in the original problem set!
- In the combustion of propane (14.1), I have forgotten to add \(O_2\) onto the reactants side.
- In the reaction of photosynthesis I have forgotten to add the \(O_2\) product.
14.1
The (corrected) equation \(\ce{C3H8 + O2-> CO2 + H2O}\) can be balanced with 4 unknown constants \(x_1, x_2, x_3, x_4\): \[x_1(\ce{C3 H8}) + x_2(\ce{O2}) \longrightarrow x_3(\ce{CO2}) + x_4(\ce{H2O})\] And then we can construct the table:
| left | right | |
| carbon | \(3x_1\) | \(x_3\) |
| hydrogen | \(8x_1\) | \(2x_4\) |
| oxygen | \(2x_2\) | \(2x_3 + x_4\) |
From which we construct the equations:
\begin{align} 3x_1-x_3 &= 0 \\ 8x_1 - 2x_4 &= 0\\ 2x_2 - 2x_3 - x_4 &= 0 \end{align}And consequently the augmented matrix:
\[\left [ \begin{array}{cccc|c} 3&0&-1&0&0\\ 8&0&0&-2&0\\ 0&2&-2&-1&0\\ \end{array}\right ] \leadsto \left [ \begin{array}{cccc|c} 1 & 0 & 0 & -\frac{1}{4} & 0 \\ 0 & 1 & 0 & -\frac{5}{4} & 0 \\ 0 & 0 & 1 & -\frac{3}{4} & 0 \\ \end{array}\right ] \]
Thus the balanced equation becomes: \[\ce{C3H8 + 5O2 -> 3CO2 + 4H2O}\]
14.2
Similarly we apply the same method to \(\ce{CO2 + H2O -> C6H12O6 + O2}\). Creating the table:
| carbon | \(1x_1\) | \(6x_3\) |
| oxygen | \(2x_1+x_2\) | \(6x_3 + 2x_4\) |
| hydrogen | \(2x_2\) | \(12x_3\) |
And thus the augmented matrix: \[\left [ \begin{array}{cccc|c} 1&0&-6&0&0\\ 2&1&-6&-2&0\\ 0&2&-12&0&0\\ \end{array}\right ]\] Which after applying Gaussian elimination, leads to: \[\left [ \begin{array}{cccc|c} 1&0&0&-1&0\\ 0&1&0&-1&0\\ 0&0&1&-\frac{1}{6}&0\\ \end{array}\right ]\]
Ultimately, the balanced equation becomes: \[\ce{6CO2 + 6H2O -> 1C6H12O6 + 6O2}\]
14.3
We apply the same method to \(\ce{HCl + Na3 -> H3PO4 + NaCl}\).
| H | \(1x_1\) | \(3x_3\) |
| Cl | \(1x_1\) | \(1x_4\) |
| Na | \(3x_2\) | \(1x_4\) |
| P | \(1x_2\) | \(1x_3\) |
| O | \(4x_2\) | \(4x_3\) |
\[\left [ \begin{array}{cccc|c} 1&0&-3&0&0\\ 1&0&0&-1&0\\ 0&3&0&-1&0\\ 0&1&-1&0&0\\ 0&4&-4&0&0 \end{array}\right ]\]
But then because rows 4 and 5 are only separated by a constant multiple, we can just ignore one of them.
\[\left [ \begin{array}{cccc|c} 1&0&0&-1&0\\ 0&1&0&-\frac{1}{3}&0\\ 0&0&1&-\frac{1}{3}&0\\ 0&0&0&0&0\\ \end{array}\right ]\]
Parametrising \(x_4\) as \(t\) and setting it to 3 for integer solutions to all \(x_i\), we get \(x_1 = 3, x_2 = 1, x_3 = 1, x_4 = 3\), and thus \[\ce{3HCl + 1Na3PO4 -> 1H3PO4 + 3NaCl}.\]
Q15
There \(\frac{6!}{3!\times 2!} = 60\) distinct arrangements in the word BANANA.
Q16
We let \(a=4, b=6, c=7\) on the triangle:
And use Heron's formula: \[A = \sqrt{s(s-a)(s-b)(s-c)},\qquad\text{ where }s=\frac{a+b+c}{2}\]
such that \(A = \sqrt{\frac{2295}{16}}\) which simplifies to \(\frac{3\sqrt{255}}{4} \approx 11.97\).
Q17
Q18
Q19
We leverage the basic projectile motion equation: \[S_y = u_y t + \frac{1}{2}a_y t^2, \] where \[\begin{align*} S_y &= \text{the vertical displacement} = 2.4\mathrm{m}\\ u_y &= \text{the initial velocity} = 40\sin{7}\\ t &= \text{time} = ?\\ a_y &= \text{vertical acceleration} = 10\mathrm{ms}^{-2}\\ \implies S_y &= 40\sin{7}t + \frac{1}{2}(10)t^2 \end{align*}\]
Solving this quadratic in \(t\) yields \(t\approx 0.359 \text{seconds}\)
Q20
20.1
\[\vec{u} + \vec{w} = \begin{bmatrix}1\\-4\end{bmatrix}\]
20.2
\[|\vec{u}+\vec{w}| = \sqrt{17} \]
20.3
\[3\vec{v}-2\vec{u}+\vec{v} = \begin{bmatrix}-8\\22\end{bmatrix}\]
Q21
\[x \equiv 7 + 30\,k, \qquad k\in\mathbb{Z}^+\]