Classical Algorithms
Try to not to use Machine Learning —Rule #1 in Google's Machine Learning Handbook
if the problem can be solved in an analysed time and space complexity we should do it classically. Machine Learning requires data.
| algorithm | time-complexity | function | style |
|---|---|---|---|
| BFS | $\mathcal{O}(V+E)$ | Shortest Path | Traversal |
| DFS | $\mathcal{O}(V+E)$ | Topo-sorting, Cycle testing, connected components | Traversal |
| Kruskal | $\mathcal{O}(E\log(V))$ | MST | Greedy |
| Prim | $\mathcal{O}((E+V)\log(V))$ | MST | Greedy |
| Dijkstra | $\mathcal{O}((E+V)\log(V))$ | Shortest Path, non-unit weights | Greedy |
| Bellman-Ford | $\mathcal{O}(VE)$ | Negative Weight SP | DP |
| Floyd-Warshall | $\mathcal{O}(V^3)$ | All Pairs SP. | DP |
| Ford-Fulkerson | $\mathcal{O}(Ef)$ | Max flow / min-cut with untethered implementation | Greedy |
| Edmond-Karp | $\mathcal{O}(VE^2)$ | Max flow with BFS. | Greedy |
testing mathjax: $\abs{5}$ (mathtools)
2 Pointers
schematic
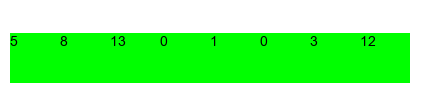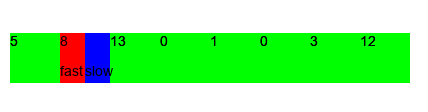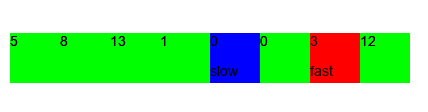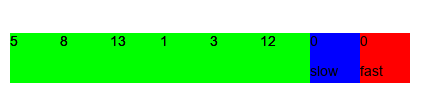
this paradigm works well on arrays, reducing the time complexity of some popular problems from $\mathcal{O}(n^2)$ to $\mathcal{O}(n)$.
there are a few flavours of this technique: fast and slow; opposite pointers, but ultimately we do keep track of two indices left and right. sometimes abbreviated to l and r in the code.
common problems that this algorithm works well on include:
- finding cycles in a linked list (fast and slow pointers)
- finding pairs
- comparing elements from opposite ends of a data structure
Sliding Window
this is a special case of the two-pointers strategy above, and maintains a fixed-window length across the array.
it can be used to solve problems of the sort:
- maximise length of substring
- maintain sum within a target value
- leetcode problem 3
it is often combined with hashmaps to keep track of the elements within the window
Binary Search
this is technically an expansion of the two pointers pattern.
it can be used on any list that has a monotonic function.
privvy to utilise any condition for sorting; e.g. T/F
def binary_search(arr: List[int], target: int) -> int:
left, right = 0, len(arr) - 1
first_true_index = -1
while left <= right:
mid = (left + right) // 2
if feasible(mid):
first_true_index = mid
right = mid -1
else:
left = mid+1
return first_true_indexwe can apply the above prototype to leetcode problem 153
Breadth First Search
this algorithm is good for finding the shortest path between two nodes.
it is worth realising that a tree is just a graph without cycles.
BFS uses a queue data-structure. we can implement bfs by using a queue which is built with a deque:
from collections import deque
def bfs_by_queue(root):
queue = deque([root])
while len(queue) > 0:
node = queue.popleft()
for child in node.children:
if OK(child):
return FOUND(child)
queue.append(child)
return NOT_FOUNDBacktracking
this is just an extension of DFS (?), with the caveat that there is no longer a pre-built structure (i.e. an underlying tree)
Dynamic Programming
this is one of the more difficult patterns (allegedly). there are two types:
top-down
back-tracking + memoisation
bottom-up
solve smallest subproblems first.
fill out a table
Depth First Search
this algorithm is better for finding a route to a vertex that is deep within the search-tree.
we use an implementation of a "stack" to execute this algorithm, but in practice we can often use recursion paired with a "call-stack"!
DFS is good for:
- exploring all paths
- detecting cycles
- memory efficient searchs
- deep searching
Heap / Priority Queue
heaps are implementations of priority queues (?)
this data structure is used to solve problems of the type: "top K" and is slightly unintuitive, because to find the top K "largest", we require a min-heap, and to find the top K "smallest", we require a max-heap:
see leetcode problems:
Divide and Conquer
Trie
this refers to the data-structure, but algorithms for insertion, deletion and search can be documented here.
there is also a relation with a Radix Tree which is a compressed version of a trie, but I'm not sure how it all connects.
Union Find
again, I am not sure where to draw the line between data-structure and algorithm here.
it seems that this is a data-structure for handling a collection of "disjoint-sets" and efficiently performs two primary operations:
- union: merging two sets and;
- find: determining which set an element belongs to
Greedy
Graph
we have already covered a couple of "graph" algorithms on this page: binary search, breadth first search, depth first search. but there are many more such algorithms:
- prim
- kruskal
-
dijkstra
dijkstra fail
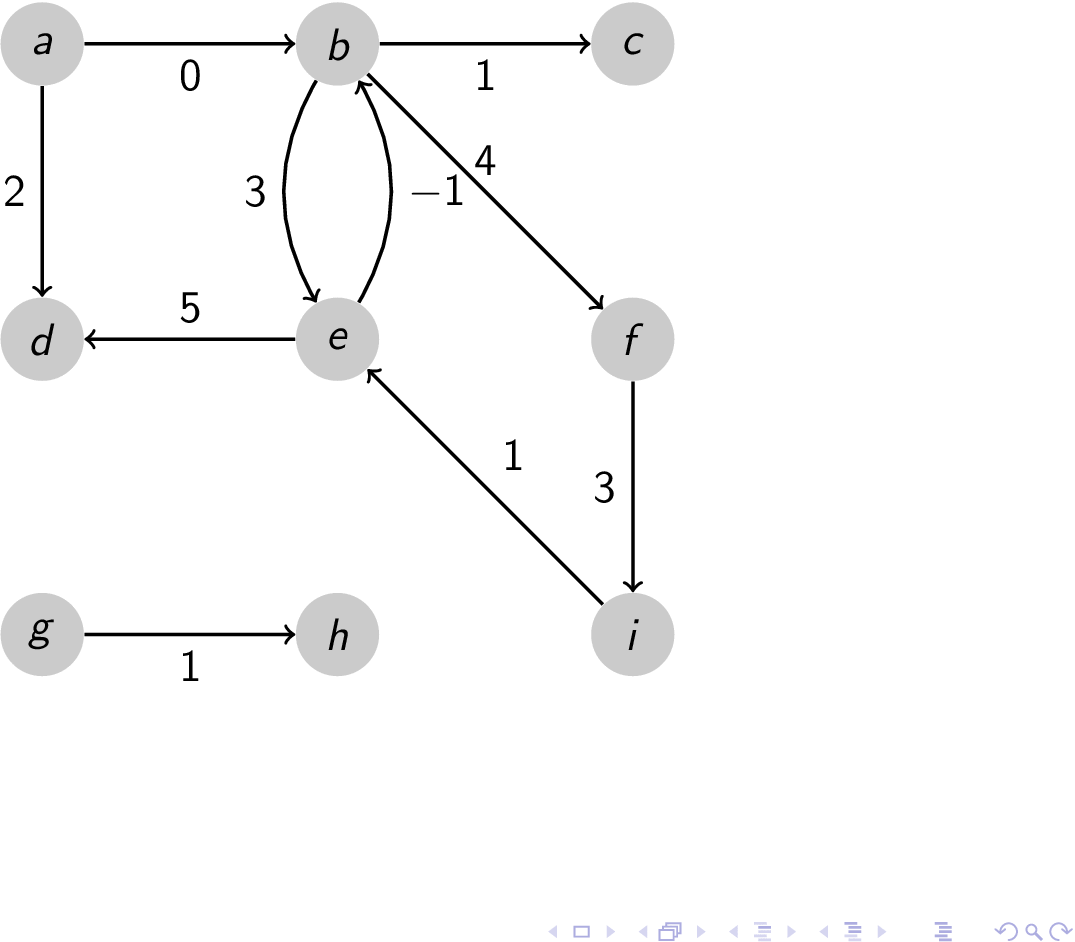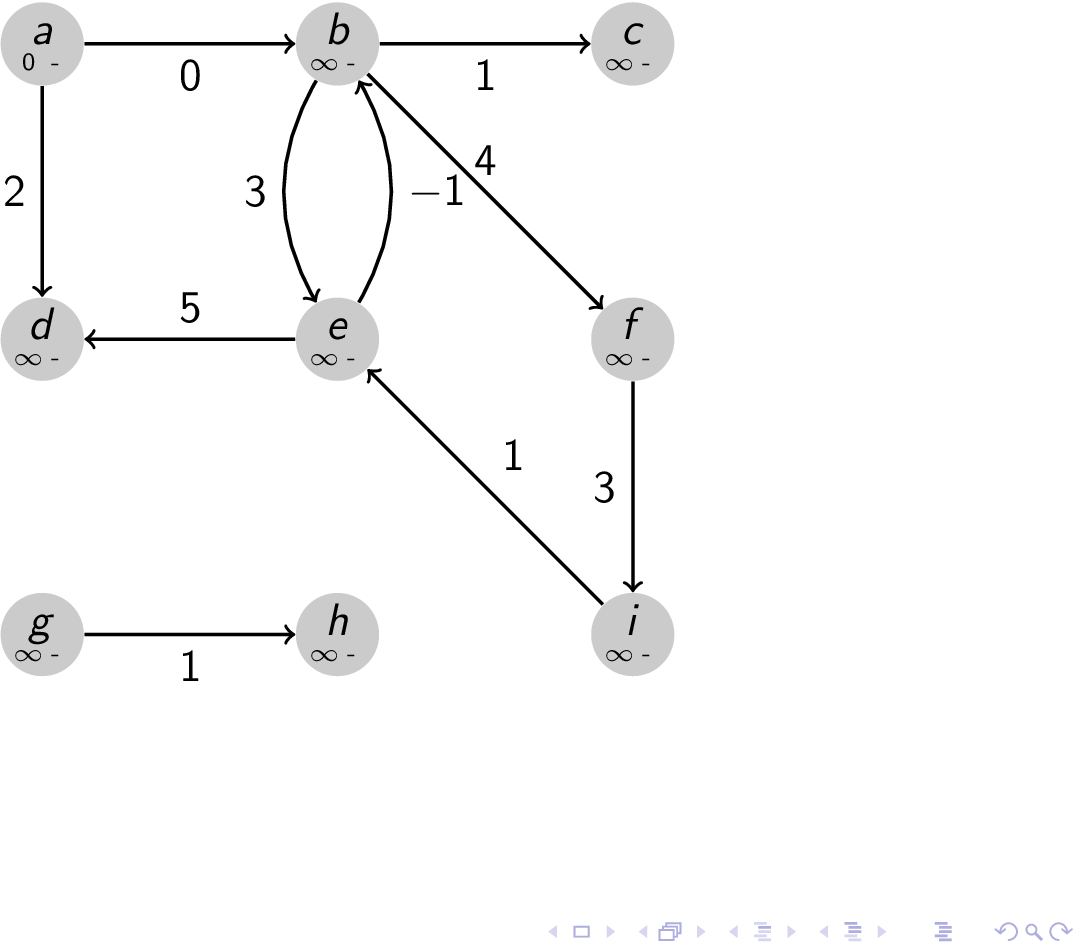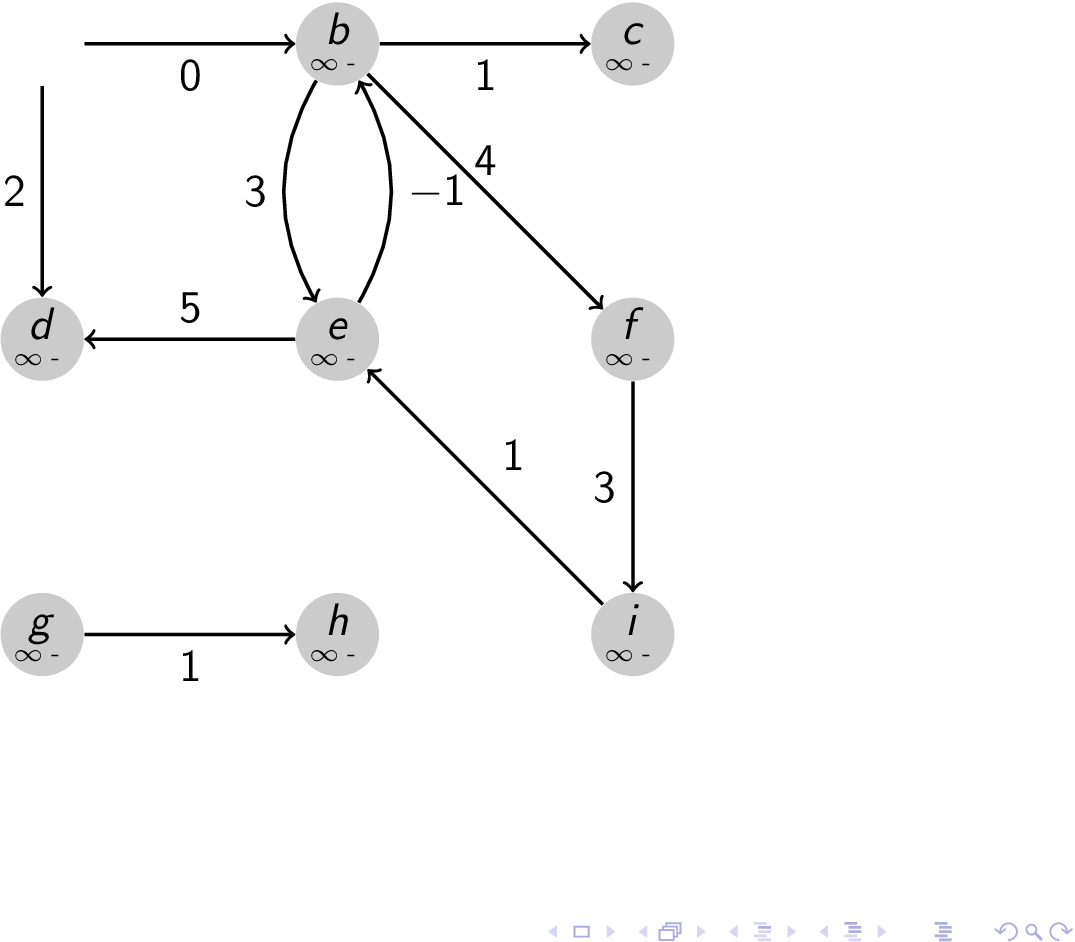
Linear Programming
a "sledgehammer" of the trade according to Dasgupta
Recursion
recursion is probably a concept that deserves at least a small amount of recognition as a concept, and designated place wherein which to place notes.
this algorithmic technique goes hand-in-hand with trees and divide and conquer
Searching
searching is one of the main concerns of graph algorithms: finding a route to a particular vertex or finding the value of a vertex itself.
we have covered binary search, breadth first search and depth first search, but we have not yet made notes about:
- heuristic searches
- a* star search
- monte carlo
Sorting
we have not covered sorting at all on this page, it seems to be one of the less examined topics in leetcode. nonetheless, it is an important and interesting application of the data structures and algorithms we know.
time complexities1
| Algorithm | Time | Space (worst) | ||
|---|---|---|---|---|
| Best | Average | Worst | ||
| quicksort | $\Omega(n\log n)$ | $\Theta(n\log n)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(\log n)$ |
| mergesort | $\Omega(n\log n)$ | $\Theta(n\log n)$ | $\mathcal{O}(n\log n)$ | $\mathcal{O}(n)$ |
| timsort | $\Omega(n)$ | $\Theta(n\log n)$ | $\mathcal{O}(n\log n)$ | $\mathcal{O}(n)$ |
| heap | $\Omega(n\log n)$ | $\Theta(n\log n)$ | $\mathcal{O}(n\log n)$ | $\mathcal{O}(1)$ |
| bubble | $\Omega(n)$ | $\Theta(n^2)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(1)$ |
| insertion | $\Omega(n)$ | $\Theta(n^2)$ | $\mathcal{O}(n\log n)$ | $\mathcal{O}(1)$ |
| selection | $\Omega(n^2)$ | $\Theta(n^2)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(1)$ |
| bucket | $\Omega(n+k)$ | $\Theta(n+k)$ | $\mathcal{O}(n^2)$ | $\mathcal{O}(n)$ |
| radix | $\Omega(nk)$ | $\Theta(nk)$ | $\mathcal{O}(nk)$ | $\mathcal{O}(n+k)$ |
bubble-sort
Footnotes
these time complexities, along with a number of others were taken from https://bigocheatsheet.com.